回归曲线图
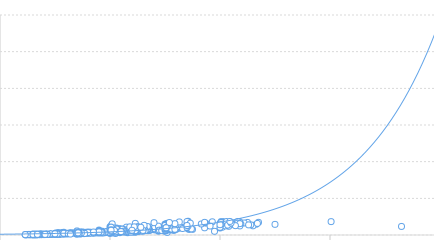
回归曲线图的简介
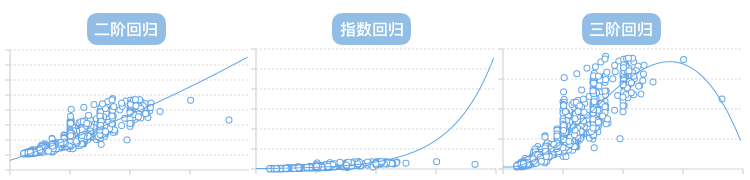
回归曲线图同统计学紧密结合,属于探索型图表,通过对样本数据进行曲线回归(非线性回归)确定两个变数间数量变化的某种特定的规则或规律。我们称图中的线为回归曲线,是最准确地贯穿图中的各个点的线,分为线性回归和非线性回归。
回归曲线图用于回归分析,其主要内容是通过试验或观测数据,寻找相关变量之间的统计规律性,再利用自变量的值有效预测因变量的可能取值。
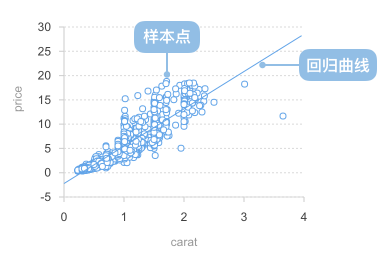
回归曲线图的构成
| 图表类型 | 回归曲线图 |
|---|---|
| 适合的数据 | 两个连续字段 |
| 功能 | 观察数据的变化趋势根据样本点 预测数据 |
| 数据与图形的映射 | 两个连续字段的分布特征元数据映射到回归线 |
| 适合的数据条数 | 暂无限制 |
回归曲线图的应用场景
例子 1:线性回归(linear regresiion)。 线性回归是最原始的回归,用来做数值类型的回归,可以利用它来构建模型并通过构件的模型来进行预测。借助可视化技术,我们可以快速判断一组数据是否属于线性回归。
比如某农业科研机构要研究最大积雪深度 x 与灌溉面积 y 之间的关系,提供的数据样本为近 10 年的数据,如下表:
| 年序 | 最大积雪深度 x(尺) | 灌溉面积 y (亩) |
|---|---|---|
| 1 | 15.2 | 28.6 |
| 2 | 10.4 | 19.3 |
| 3 | 21.2 | 40.5 |
| 4 | 18.6 | 35.6 |
| 5 | 26.4 | 48.9 |
| 6 | 23.4 | 45.0 |
| 7 | 13.5 | 29.2 |
| 8 | 16.7 | 34.1 |
| 9 | 24.0 | 46.7 |
| 10 | 19.1 | 37.4 |
借助 DataSet 的回归统计Transform(regression),绘制如下图表:
具体的回归分析过程不在这里详述,具体可阅读: 数理统计知识整理——回归分析与方差分析
例子 2:非线性回归。 一些常用的非线性回归曲线。